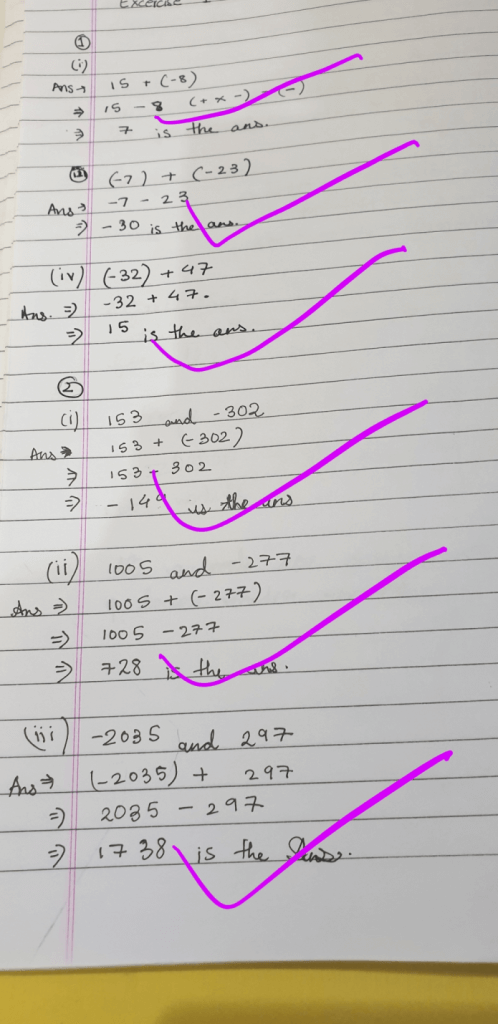Integers

INTEGERS :

We have learnt about natural and whole numbers in the previous chapters . But when we subtract a greater whole number from a smaller whole number, then the difference will not be a whole numbers. Hence , there is a need to extend the number system to include such numbers.

In our day to day life , we often come across many situation involving the use of opposite .Some of these are discussed below.

Temperature:  During the winter sea 7th Class Mathematics BLOG son , the minimum temperature on a particular day.Say in Chennai , may be 20 ⁰ C. This means that the temperature in Chennai is higher than the melting point of ice, which is 0 ⁰ C . On the same day , the minimum temperature in Shimla may be 5 ⁰ C below 0 ⁰ .  How do we represent this? This can be represented as – 5 ⁰ C, read as minus five degree centigrade .

What is an Integer?

An integer is a whole number. This means an integer is any number that is NOT expressed via a decimal or a fraction.

Integers include all negative whole numbers, all positive whole numbers, and zero.

Examples of Integers:

-55, -2, 0, 14, 10,699

NOT  Integers

Π, 2/3, 0.087

Positive and Negative Integers

A number line is used to demonstrate how numbers relate to each other and to zero. All numbers to the right of zero are positive numbers. All numbers to the left of zero are negative numbers.

Operation on Integers

Facts about how to Add and Subtract Integers on the Number Line

1. If we add a positive integer, we go to the right.

2. If we add a negative integer, we go to the left.

Properties of Multiplication of Integers

Closure under Multiplication

For every integer a and b, a×b=Integer

Commutative Property of Multiplication
For every integer a and b, a×b=b×a

Multiplication by Zero
For every integer a, a×0=0×a=0

Multiplicative Identity
For every integer a, a×1=1×a=a. Here 1 is the multiplicative identity for integers.

Associative property of Multiplication
For every integer a, b  and c,  (a×b)×c=a×(b×c)

Distributive Property of Integers
Under addition and multiplication,  integers show the distributive property.
i.e., For every integer a, b  and c,  a×(b+c)=a×b+a×c

These properties make calculations easier.

Multiplication Of Integers

Multiplication of two integers is the repeated addition.

Example

• 3 × (-2) = three times (-2) = (-2) + (-2) + (-2) = – 6
• 3 × 2 =  three times 2 = 2 + 2 + 2 = 6